Формула суммы геометрической прогрессии

формула суммы геометрической прогрессии

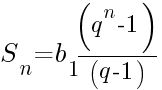
формула суммы геометрической прогрессии

Геометрическая прогрессия - это последовательность чисел b1, b2, и т.д., каждое из которых равно предыдущему, умноженному на знаменатель прогрессии - q. 

bn =b1qn-1

n - это общее число членов прогрессии. Очевидно, что если q =1, то получается частный случай формулы:

S=nb1. 


Существует легенда о том, что один царь решил наградить мудреца за то, что тот научил его играть в шахматы. Мудрец просил царя положить на первую клетку шахматной доски пшеничное зернышко, на каждую следующую класть в 2 раза больше. На доске для шахмат 64 клетки.

Получается такая огромная цифра, что у царя просто не хватило запасов.

Еще формулы из базы:

серная кислота, работы, объема конуса, объем цилиндра, логарифмов, суммы кубов, сокращенного умножения, щелочей, площади трапеции, сопротивление, производных, соляная кислота, давления, соли, оксида, кислот, разности кубов, лимонной кислоты, этиловый спирт, скорости, объема, энергия фотона, общая формула алкенов, массы, тангенса, объем призмы, магнитный поток, средняя скорость, углекислый газ, емкость конденсатора, ЭДС, угольная кислота
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях: