Формулы тригонометрии

формулы тригонометрии

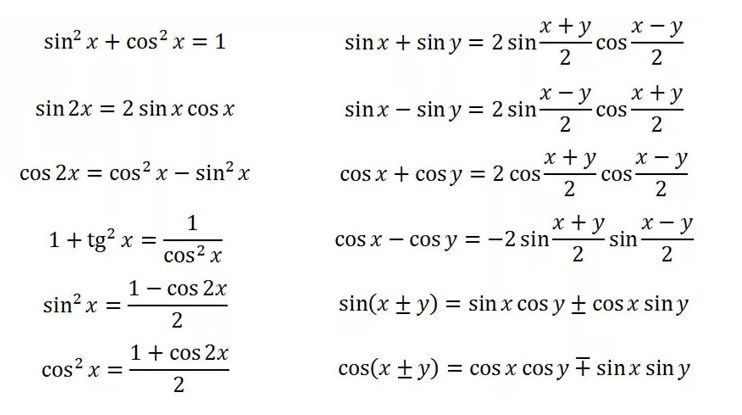
Формулы тригонометрии по сути это основные тригонометрические тождества. Используя данные формулы можно существенно упростить процесс решения задач, в которых присутствуют тригонометрические функции.


Пример использования формул тригонометрии

Дано уравнение:
sin2x + cos2x = 1
Задача: найти корни.
sin2x + cos2x -1 =0 
Используя форумы раскладываем 1 и тригонометрические функции двойного угла.
2sinxcosx + cos2x - sin2x - sin2x -cos2x = 0
2sinxcosx - 2sin2x = 0
2sinx(cosx-sinx)=0

Находим корни уравнения
sinx =0 или cosx-sinx=0
x1=πn
sinx=cosx 
tgx=1
x2 = π/2 a+πn
Ответ: πn,  π/2 a+πn

Еще формулы из базы:

сила трения, площади квадрата, общая формула алкана, длина волны, мела, производных, глицерин, понижения степени, давления, суммы кубов, соли, этанол, этиловый спирт, фосфорная кислота, сахарозы, глюкоза, плотности, напряженности, объема шара, площади треугольника, сокращенного умножения, ЭДС, средняя скорость, массы, энергия фотона, угольная кислота, емкость конденсатора, объем призмы, углекислый газ, магнитный поток, тангенса, общая формула алкенов
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях: